这是一个句子测试

4
19
2016
0

SDOI2016膜蛤记

有幸膜到了贵省的题目，感到不明觉厉，于是水了一发题解来骗访客量。

T1

给定n、m、k、p，求：

[tex]\sum_{i=0}^{n-1}\sum_{j=0}^{m-1}max(i\ xor\ j-k,0)[/tex]

答案对p取模。

显然可以数位dp，令dp[i][0/1][0/1][0/1]表示前i位，小于/等于n，小于/等于m，异或值大于/等于k的方案数，Dp[i][0/1][0/1][0/1]表示满足限制的异或值之和，转移只要分类讨论一下就行辣！

#include<cstdio>
#include<algorithm>
#include<cstring>
typedef long long ll;
using namespace std;
int cas,i,j,k,l,p,q,mod,dign[64],digm[64],digk[64];
ll n,m,K,mi[64],dp[65][2][2][2],Dp[65][2][2][2];
int main(){
	scanf("%d",&cas);
	while (cas--){
		scanf("%lld%lld%lld%d",&n,&m,&K,&mod);
		mi[0]=1;for (i=1;i<=63;i++)mi[i]=mi[i-1]*2%mod;
		memset(dp,0,sizeof dp);
		memset(Dp,0,sizeof Dp);
		for (i=0;i<=63;i++){
			if (n&(1ll<<(63-i)))dign[i]=1;else dign[i]=0;
			if (m&(1ll<<(63-i)))digm[i]=1;else digm[i]=0;
			if (K&(1ll<<(63-i)))digk[i]=1;else digk[i]=0;
		}
		dp[0][1][1][1]=1;
		for (i=0;i<=63;i++)
			for (j=0;j<=1;j++)
				for (k=0;k<=1;k++)
					for (l=0;l<=1;l++)
						for (p=0;p<=1;p++)
							for (q=0;q<=1;q++)
								if ((!j||p<=dign[i])&&(!k||q<=digm[i])&&(!l||(p^q)>=digk[i])){
									dp[i+1][j&(p==dign[i])][k&(q==digm[i])][l&((p^q)==digk[i])]=(dp[i+1][j&(p==dign[i])][k&(q==digm[i])][l&((p^q)==digk[i])]+dp[i][j][k][l])%mod;
									Dp[i+1][j&(p==dign[i])][k&(q==digm[i])][l&((p^q)==digk[i])]=(Dp[i+1][j&(p==dign[i])][k&(q==digm[i])][l&((p^q)==digk[i])]+Dp[i][j][k][l]+dp[i][j][k][l]*mi[63-i]*(p^q))%mod;
								}
		printf("%lld\n",(Dp[64][0][0][0]-dp[64][0][0][0]*(K%mod)%mod+mod)%mod);
	}
}

T2

有n种数，每种数字为ai，有bi个，权值为ci。若两个数字满足ai/aj是质数，那么就可以配对并获得ci*cj的价值（两个数字只可配对一次）。求在获得总价值大于0的情况下，最多能配对几次。

考虑ai/aj是质数这个奥妙重重的性质。如果对ai进行质因数分解，若指数之和为奇数，显然只能和指数之和为偶数的数配对，于是原图就变成了一个二分图。

那么可以建出经典的网络流模型，黑白染色后，源连黑点，流量为bi，黑点连可匹配的白点，流量inf，白点连汇，流量为bi。

对于价值的限制，可以对流量为inf的边加上ci*cj的费用，那么跑费用流时会将价值大的先跑过去，只要不断跑流判一下临界值即可。

#include<cstdio>
#include<algorithm>
#include<cstring>
typedef long long ll;
using namespace std;
const int M=200010;
const int inf=1<<29;
int n,i,j,cnt,edgenum,Ans;
int a[M],b[M],prime[M],ss[M],head[M],vet[M],next[M],flag[M],size[M],h[M],rem[M],pre[M][2];
ll ans,c[M],dis[M],len[M];
int calc(int x){
	int ans=0;
	for (int i=1;i<=cnt;i++)
		while (!(x%prime[i])){
			x/=prime[i];
			ans++;
		}
	if (x!=1)ans++;
	return ans;
}
void addedge(int x,int y,int z,ll w){
	vet[++edgenum]=y;
	next[edgenum]=head[x];
	head[x]=edgenum;
	size[edgenum]=z;
	len[edgenum]=w;
	vet[++edgenum]=x;
	next[edgenum]=head[y];
	head[y]=edgenum;
	size[edgenum]=0;
	len[edgenum]=-w;
}
int spfa(){
	for (int i=1;i<=n+1;i++)dis[i]=-(1ll<<40);
	int l=1,r=1;
	flag[0]=1;rem[0]=inf;
	while (l<=r){
		int u=h[l];
		for (int e=head[u];e;e=next[e]){
			int v=vet[e];
			if (size[e]&&dis[v]<dis[u]+len[e]){
				dis[v]=dis[u]+len[e];
				pre[v][0]=u;
				pre[v][1]=e;
				rem[v]=min(rem[u],size[e]);
				if (!flag[v]){
					flag[v]=1;
					h[++r]=v;
				}
			}
		}
		l++;
		flag[u]=0;
	}
	if (dis[n+1]==-(1ll<<40))return 0;
	if (ans+dis[n+1]*rem[n+1]<0){
		Ans-=ans/dis[n+1];
		return 0;
	}
	ans+=dis[n+1]*rem[n+1];
	Ans+=rem[n+1];
	int u=n+1;
	while (u){
		size[pre[u][1]]-=rem[n+1];
		size[pre[u][1]^1]+=rem[n+1];
		u=pre[u][0];
	}
	return 1;
}
int Abs(int x){
	if (x<0)return -x;else return x;
}
int main(){
	edgenum=1;
	scanf("%d",&n);
	for (i=1;i<=n;i++)scanf("%d",&a[i]);
	for (i=1;i<=n;i++)scanf("%d",&b[i]);
	for (i=1;i<=n;i++)scanf("%lld",&c[i]);
	for (i=2;i<=34000;i++){
		if (!ss[i])prime[++cnt]=i;
		for (j=1;j<=cnt&&i*prime[j]<=34000;j++){
			ss[i*prime[j]]=1;
			if (!(i%prime[j]))break;
		}
	}
	for (i=1;i<=n;i++)
		for (j=1;j<=n;j++)
			if ((!(a[i]%a[j])||!(a[j]%a[i]))&&calc(a[i])&1&&Abs(calc(a[i])-calc(a[j]))==1)addedge(i,j,inf,c[i]*c[j]);
	for (i=1;i<=n;i++)
		if (calc(a[i])&1)addedge(0,i,b[i],0);
			else addedge(i,n+1,b[i],0);
	while (spfa());
	printf("%d\n",Ans);
}

T3

有一棵树，每次操作对u~v的路径上的每个点x，点权对a*dis(u,x)+b取min，询问u~v的最小点权。

发现a*dis(u,x)+b这个表达式实在是太丑了，考虑化简一下。

对于u~lca(u,v)上的点，a*dis(u,x)+b=-a*dep[x]+a*dep[u]+b。

对于v~lca(u,v)上的点，a*dis(u,x)+b=a*dep[x]+a*dep[u]+b-2*dep[lca(u,v)]。

那么对于一个点的值就变成了一个一次函数a*dep[u]+b。

考虑树链剖分，一段重链的dep显然是单调递增的，那么只要用线段树维护一个区间的若干直线在每个部分的最小值即可。

假设一个区间上躺着一个标记a1*x+b1，又新加了一个标记a2*x+b2，若特判掉某个标记始终更优的情况，那么会存在一个分界点满足两半的最优情况通过不同的标记取到。那么就可以判断哪个标记被完全包含在该节点的左右儿子中，然后下传即可。（这就是线段树维护半平面交的过程）

至于询问，可以直接利用永久化标记的方法更新。

#include<cstdio>
#include<algorithm>
#include<cstring>
typedef long long ll;
using namespace std;
const int M=200010;
int n,m,i,x,y,z,p,q,opt,edgenum,time;
int head[M],vet[M],next[M],len[M],dep[M],fa[M][20],size[M],son[M],flag[M],tid[M],pre[M],top[M],ance[M];
ll dis[M];
struct node{int tag;ll k,b,w;}tree[M<<2];
void addedge(int x,int y,int z){
	vet[++edgenum]=y;
	next[edgenum]=head[x];
	head[x]=edgenum;
	len[edgenum]=z;
}
int lca(int x,int y){
	if (dep[x]<dep[y])swap(x,y);
	int t=dep[x]-dep[y];
	for (int i=0;i<=16;i++)
		if (t&(1<<i))x=fa[x][i];
	for (int i=16;i>=0;i--)
		if (fa[x][i]!=fa[y][i])x=fa[x][i],y=fa[y][i];
	if (x==y)return x;
	return fa[x][0];
}
void dfs(int u,int pre){
	size[u]=1;fa[u][0]=pre;
	for (int i=1;i<=16;i++)
		fa[u][i]=fa[fa[u][i-1]][i-1];
	for (int e=head[u];e;e=next[e]){
		int v=vet[e];
		if (v==pre)continue;
		dep[v]=dep[u]+1;
		dis[v]=dis[u]+len[e];
		dfs(v,u);
		size[u]+=size[v];
		if (!son[u]||size[v]>size[son[u]])son[u]=v;
	}
}
void Dfs(int u,int ance){
	flag[u]=1;
	tid[u]=++time;pre[time]=u;top[u]=ance;
	if (son[u])Dfs(son[u],ance);
	for (int e=head[u];e;e=next[e]){
		int v=vet[e];
		if (flag[v])continue;
		Dfs(v,v);
	}
}
void pushup(int p,int l,int r){
	int L=p<<1,R=p<<1^1;
	if (l<r)tree[p].w=min(tree[L].w,tree[R].w);
		else tree[p].w=123456789123456789ll;
	if (tree[p].tag)tree[p].w=min(tree[p].w,min(dis[pre[l]]*tree[p].k,dis[pre[r]]*tree[p].k)+tree[p].b);
}
void UPDATE(int l,int r,int p,ll k,ll b){
	if (!tree[p].tag){
		tree[p].tag=1;tree[p].k=k;tree[p].b=b;
	}else{
		int mid=l+r>>1;
		ll x1=k*dis[pre[l]]+b,x2=k*dis[pre[r]]+b,y1=tree[p].k*dis[pre[l]]+tree[p].b,y2=tree[p].k*dis[pre[r]]+tree[p].b;
		if (x1<=y1&&x2<=y2){
			tree[p].k=k;tree[p].b=b;
		}else if (x1>=y1&&x2>=y2)return;
			else if (k<tree[p].k){
				ll tmp=(b-tree[p].b)/(tree[p].k-k)+1;
				if (tmp<=dis[pre[mid]]){
					swap(k,tree[p].k);swap(b,tree[p].b);
					UPDATE(l,mid,p<<1,k,b);
				}else UPDATE(mid+1,r,p<<1^1,k,b);
			}else{
				ll tmp=(tree[p].b-b-1)/(k-tree[p].k);
				if (tmp>dis[pre[mid]]){
					swap(k,tree[p].k);swap(b,tree[p].b);
					UPDATE(mid+1,r,p<<1^1,k,b);
				}else UPDATE(l,mid,p<<1,k,b);
			}
	}
	pushup(p,l,r);
} 
void update(int x,int y,int l,int r,int p,ll k,ll b){
	if (x==l&&y==r){
		UPDATE(x,y,p,k,b);
		return;
	}
	int mid=l+r>>1;
	if (y<=mid)update(x,y,l,mid,p<<1,k,b);
		else if (x>mid)update(x,y,mid+1,r,p<<1^1,k,b);
			else {update(x,mid,l,mid,p<<1,k,b);update(mid+1,y,mid+1,r,p<<1^1,k,b);}
	pushup(p,l,r);
}
ll query(int x,int y,int l,int r,int p){
	if (x==l&&y==r)return tree[p].w;
	int mid=l+r>>1;
	ll ans=123456789123456789ll;
	if (tree[p].tag)ans=min(ans,min(dis[pre[x]]*tree[p].k,dis[pre[y]]*tree[p].k)+tree[p].b);
	if (y<=mid)return min(ans,query(x,y,l,mid,p<<1));
		else if (x>mid)return min(ans,query(x,y,mid+1,r,p<<1^1));
			else return min(ans,min(query(x,mid,l,mid,p<<1),query(mid+1,y,mid+1,r,p<<1^1)));
}
void Update(int x,int y,ll k,ll b){
	while (top[x]!=top[y]){
		update(tid[top[x]],tid[x],1,n,1,k,b);
		x=fa[top[x]][0];
	}
	update(tid[y],tid[x],1,n,1,k,b);
}
ll Query(int x,int y){
	ll ans=123456789123456789ll;
	while (top[x]!=top[y]){
		ans=min(ans,query(tid[top[x]],tid[x],1,n,1));
		x=fa[top[x]][0];
	}
	ans=min(ans,query(tid[y],tid[x],1,n,1));
	return ans;
}
int main(){
	scanf("%d%d",&n,&m);
	for (i=1;i<n;i++){
		scanf("%d%d%d",&x,&y,&z);
		addedge(x,y,z);
		addedge(y,x,z);
	}
	dfs(1,0);
	Dfs(1,1);
	for (i=1;i<=n<<2;i++)tree[i].w=123456789123456789ll;
	for (i=1;i<=m;i++){
		scanf("%d",&opt);
		if (opt==1){
			scanf("%d%d%d%d",&x,&y,&p,&q);
			int z=lca(x,y);
			Update(x,z,-p,dis[x]*p+q);
			Update(y,z,p,dis[x]*p-dis[z]*p*2+q);
		}else{
			scanf("%d%d",&x,&y);
			int z=lca(x,y);
			printf("%lld\n",min(Query(x,z),Query(y,z)));
		}
	}
}

T4

求串S的每个前缀中不同的子串个数。

首先将S倒过来跑后缀数组，那么求前缀[1,i]的不同子串数就转化为求后缀[i,n]的不同子串数。如果在这之前已经求出[i+1,n]的不同子串数，那么只要求出后缀[i,n]与后缀集合[i+1,n]的最长LCP即可。

那么只要在sa上二分+rmq求出相邻的两个后缀然后再询问height就阔以辣！

#include<cstdio>
#include<algorithm>
#include<cstring>
using namespace std;
const int M=100010;
int n,i,j;
long long ans;
int a[M],b[M],A[M],wa[M],wb[M],wc[M],wd[M],rank[M],sa[M],height[M][20],Sa[M][20],log[M];
bool cmp(int *r,int a,int b,int l){return r[a]==r[b]&&r[a+l]==r[b+l];}
void getsa(int *r,int *sa,int n,int m){
	int *x=wa,*y=wb,j,p;
	for (i=0;i<n;i++)wc[x[i]=r[i]]++;
	for (i=1;i<m;i++)wc[i]+=wc[i-1];
	for (i=n-1;i>=0;i--)sa[--wc[x[i]]]=i;
	for (j=1,p=1;p<n;j<<=1,m=p){
		p=0;
		for (i=n-j;i<n;i++)y[p++]=i;
		for (i=0;i<n;i++)if (sa[i]>=j)y[p++]=sa[i]-j;
		for (i=0;i<n;i++)wd[i]=x[y[i]];
		for (i=0;i<m;i++)wc[i]=0;
		for (i=0;i<n;i++)wc[wd[i]]++;
		for (i=1;i<m;i++)wc[i]+=wc[i-1];
		for (i=n-1;i>=0;i--)sa[--wc[wd[i]]]=y[i];
		swap(x,y);p=1;x[sa[0]]=0;
		for (i=1;i<n;i++)x[sa[i]]=cmp(y,sa[i-1],sa[i],j)?p-1:p++;
	}
}
void getheight(int *r,int *sa,int n){
	int i,j,k=0;
	for (i=1;i<=n;i++)rank[sa[i]]=i;
	for (i=0;i<n;height[rank[i++]][0]=k){
		if (k)k--;
		j=sa[rank[i]-1];
		while (r[i+k]==r[j+k])k++;
	}
}
int query(int l,int r){
	int t=log[r-l+1];
	return max(Sa[l][t],Sa[r-(1<<t)+1][t]);
}
int Query(int l,int r){
	int t=log[r-l+1];
	return min(height[l][t],height[r-(1<<t)+1][t]);
}
int main(){
	log[0]=-1;for (i=1;i<=100000;i++)log[i]=log[i>>1]+1;
	scanf("%d",&n);
	for (i=1;i<=n;i++){
		scanf("%d",&a[i]);
		A[i]=a[i];
		b[i]=a[i];
	}
	sort(A+1,A+n+1);
	int cnt=unique(A+1,A+n+1)-A-1;
	for (i=n;i>=1;i--)a[n-i]=lower_bound(A+1,A+cnt+1,b[i])-A;
	a[n]=0;
	getsa(a,sa,n+1,n+1);
	getheight(a,sa,n);
	for (i=1;i<=n;i++){sa[i]++;Sa[i][0]=sa[i];}
	for (i=1;i<=n;i++)rank[sa[i]]=i;
	for (j=1;j<=16;j++)
		for (i=1;i<=n-(1<<j)+1;i++){
			Sa[i][j]=max(Sa[i][j-1],Sa[i+(1<<(j-1))][j-1]);
			height[i][j]=min(height[i][j-1],height[i+(1<<(j-1))][j-1]);
		}
	for (i=n;i>=1;i--){
		ans+=n-i+1;
		int l=1,r=rank[i]-1;
		while (l<r){
			int mid=l+r+1>>1;
			if (query(mid,rank[i]-1)>i)l=mid;else r=mid-1;
		}
		int tmp=0;
		if (query(l,rank[i]-1)>i)tmp=Query(l+1,rank[i]);
		l=rank[i]+1,r=n;
		while (l<r){
			int mid=l+r>>1;
			if (query(rank[i]+1,mid)>i)r=mid;else l=mid+1;
		}
		if (query(rank[i]+1,l)>i)tmp=max(tmp,Query(rank[i]+1,l));
		ans-=tmp;
		printf("%lld\n",ans);
	}
}

T5

求恰好m个位置满足a[i]=i的排列a的个数。

答案就是：[tex]C_{n}^{m}*f[n-m],f[i]=f[i-1]*i+(-1)^i[/tex]

其中f[i]为错排公式的递推式。

#include<cstdio>
#include<algorithm>
#include<cstring>
typedef long long ll;
using namespace std;
const int M=100010;
const int mod=1000000007;
int cas,i,n,m;
ll mi[M],ny[M],f[M];
ll quickmi(ll x,ll y){
	ll ans=1;
	while (y){
		if (y&1)ans=ans*x%mod;
		x=x*x%mod;
		y>>=1;
	}
	return ans;
}
ll c(int x,int y){
	return mi[x]*ny[y]%mod*ny[x-y]%mod;
}
int main(){
	mi[0]=1;ny[0]=1;f[0]=1;
	for (i=1;i<=1000000;i++){
		mi[i]=mi[i-1]*i%mod;
		ny[i]=quickmi(mi[i],mod-2);
		if (i&1)f[i]=(f[i-1]*i-1)%mod;
			else f[i]=(f[i-1]*i+1)%mod;
	}
	scanf("%d",&cas);
	while (cas--){
		scanf("%d%d",&n,&m);
		printf("%lld\n",c(n,m)*f[n-m]%mod);
	}
}

T6

将一个序列分成m段，令Xi表示序列每一段的和，最小化X的方差。

那么有：

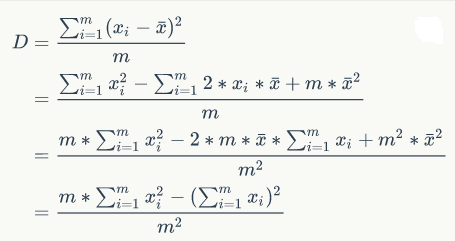
减去的部分是常数，那么只要dp前面的部分即可。

令dp[i][j]表示前i个元素分j段的最小值，显然：

[tex]dp[i][j]=min(dp[k][j]+(\sum^{i}_{p=k}x[p])^2)[/tex]

经典的分段平方和问题，可以用单调队列优化。

#include<cstdio>
#include<algorithm>
#include<cstring>
typedef long long ll;
using namespace std;
int n,m,i,j,l[10010],r[10010],h[3010][3010];
ll s[10010],dp[3010][3010];
int calc(int x,int i,int j,int k){
	if ((dp[j][x]-dp[i][x]+s[j]*s[j]-s[i]*s[i])*(s[k]-s[j])>(dp[k][x]-dp[j][x]+s[k]*s[k]-s[j]*s[j])*(s[j]-s[i]))return 1;else return 0;
}
int main(){
	scanf("%d%d",&n,&m);
	for (i=1;i<=n;i++){
		scanf("%lld",&s[i]);
		s[i]+=s[i-1];
	}
	for (i=0;i<=n;i++)l[i]=1;
	r[0]=1;h[0][1]=0;
	for (i=1;i<=n;i++)
		for (j=1;j<=m&&j<=i;j++){
			int p=h[j-1][l[j-1]],q=h[j-1][l[j-1]+1];
			while (l[j-1]<r[j-1]&&s[i]*(s[q]-s[p])*2>dp[q][j-1]-dp[p][j-1]+s[q]*s[q]-s[p]*s[p]){
				l[j-1]++;
				p=q;
				q=h[j-1][l[j-1]+1];
			}
			p=h[j-1][l[j-1]];
			dp[i][j]=dp[p][j-1]+(s[i]-s[p])*(s[i]-s[p]);
			while (l[j]<r[j]&&calc(j,h[j][r[j]-1],h[j][r[j]],i))r[j]--;
			h[j][++r[j]]=i;
		}
	printf("%lld\n",dp[n][m]*m-s[n]*s[n]);
}
Category: 蒟蒻的膜蛤记 | Tags: | Read Count: 953
Small_feed 评论 (0)

登录 *


loading captcha image...
(输入验证码)
or Ctrl+Enter

Host by is-Programmer.com | Power by Chito 1.3.3 beta | Theme: Aeros 2.0 by TheBuckmaker.com